Hoe hoog is de tafel? De opdracht die gegeven wordt in een basisschoolklas in China daagt je uit

Van tijd tot tijd verschijnen er wiskundige quizzen op het net die veel mensen in de problemen brengen. Ondanks de moeilijkheid beginnen veel enthousiastelingen, zodra ze de opdracht zien, na te denken over hoe ze het kunnen oplossen. Velen beschouwen deze tests als echte uitdagingen tegen zichzelf. Ze verspillen geen tijd, ze wapenen zich met pen en papier, schrijven het probleem op en beginnen na te denken, voeren alle mogelijke berekeningen uit tot er een lampje gaat branden en vanaf dat moment is alles gemakkelijker. Het enige dat nodig is, is de juiste intuïtie.
Zodra velen dit logisch-wiskundige probleem, voorgesteld aan een basisschoolklas in China, op het web hebben zien circuleren, verspilden ze geen tijd en probeerden ze het op te lossen. De besten van de klas hebben gefaald. Het is dan ook geen gemakkelijke opdracht, er zijn er velen geweest die het resultaat niet hebben gevonden. Zou jij in staat zijn het op te lossen?
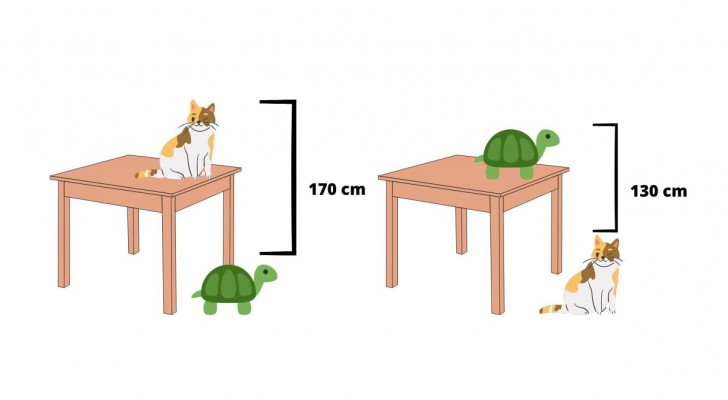
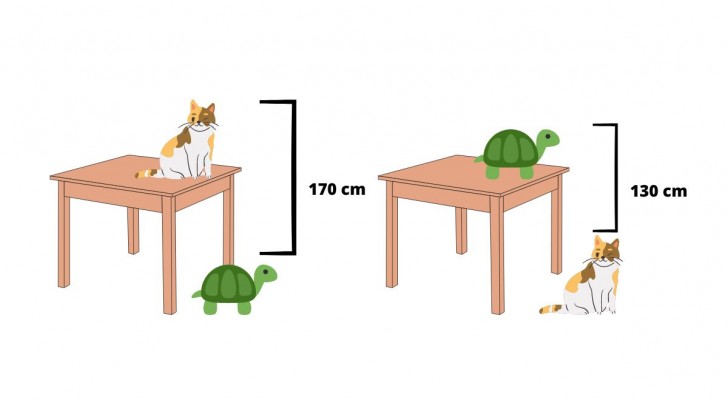
De opdracht van het probleem luidt: "vind de hoogte van de tafel, wetende dat de afstand tussen de kop van de kat op de tafel en de schildpad op de grond 170 cm is, terwijl de afstand tussen de kop van de schildpad op de tafel en de kop van de kat op de grond 130 cm is”.
Iedereen die het heeft geprobeerd, heeft zijn eigen interpretatie van het probleem gegeven, denkend de juiste oplossing te hebben gevonden. Alle resultaten waren echter niets meer dan veronderstellingen. Om deze redenen hebben experts deze test uitgevoerd om een duidelijke uitleg te geven, om iedereen de oplossing te geven. Er zijn twee soorten redeneringen: een algebraïsche en een visuele.
Algebraïsche methode

Algebraïsche methode: beide figuren kunnen worden omgezet in vergelijkingen. De eerste wordt: h. kat + h. tafel - h. schildpad = 170. (h. staat voor hoogte). De tweede kan echter getranscribeerd worden als: h. schildpad + h. tafel - h. kat = 130.
In de algebra kunnen twee vergelijkingen bij elkaar worden opgeteld: aangezien h. kat en h. schildpad tegengestelde tekens hebben in de twee vergelijkingen, heffen ze zichzelf op. De resulterende vergelijking is: 2(h. tafel) = 300, waardoor één h. tafel = 150.
Visuele methode
Visuele methode: de tweede manier om de vraag op te lossen is door visueel te denken. Stel je je eens voor dat je de twee afbeeldingen over elkaar heen kunt leggen, waardoor de basis van de eerste tafel (die aan de linkerkant) samenvalt met het oppervlak van de tweede (met andere woorden, de afbeelding links boven de rechter plaatsen). Uit deze nieuwe figuur zal het mogelijk zijn om visueel te begrijpen dat de som van de hoogten 130 cm en 170 cm exact overeenkomt met de hoogte van de twee boven elkaar geplaatste tafels, d.w.z. 300 cm. Nu kun je delen door twee om de hoogte van de enkele tafel te vinden.
Wist je het op te lossen? Welke methode heb je gebruikt?





